Picture a Chinese restaurant. People come in one at a time, and decide where to sit. The first person picks a table. Everyone afterwards picks a table according to how many people are currently at each table - popular tables continue to gain popularity.
The probability of picking a particular occupied table is
The probability of picking an empty table is
Let’s walk through a short example:
Bob walks in, sits at table 1. Jim walks in; what table does he sit at? According to our equations, $$p(\text{sit with Bob}) = \frac{1}{2}$$ $$p(\text{sit at a new table}) = \frac{1}{2}$$ Let's say he sits at a new table, and Cameron walks in. $$p(\text{sit with Bob}) = \frac{1}{3}$$ $$p(\text{sit with Jim}) = \frac{1}{3}$$ $$p(\text{sit at a new table}) = \frac{1}{3}$$ He sits with Jim. Shauna walks in. $$p(\text{sit with Bob}) = \frac{1}{4}$$ $$p(\text{sit with Jim and Cameron}) = \frac{2}{4}$$ $$p(\text{sit at a new table}) = \frac{1}{4}$$
Now let's take a look at a simulation using [Church](https://probmods.org/index.html):
```scheme
(define (seating-probabilities seating-arrangement)
(let ((total-seated (sum seating-arrangement)))
(map (lambda (people-seated)
(if (eq? people-seated 0)
(/ 1 (+ total-seated 1))
(/ people-seated (+ total-seated 1))))
seating-arrangement)))
(define (ensure-empty-table seating-arrangement)
(if (member 0 seating-arrangement)
seating-arrangement
(pair 0 seating-arrangement))
)
(define (seat-person seating-arrangement)
(let* ((table-numbers (range 0 (- (length seating-arrangement) 1)))
(chosen-seat (multinomial table-numbers
(seating-probabilities seating-arrangement)))
(new-arrangement (update-list seating-arrangement
chosen-seat
(+ 1 (list-ref seating-arrangement
chosen-seat)))))
(ensure-empty-table new-arrangement)))
(define (seat-people-inner number-of-people-waiting seating-arrangement)
(if (eq? number-of-people-waiting 0)
seating-arrangement
(seat-people-inner (- number-of-people-waiting 1)
(seat-person seating-arrangement))))
(define (seat-people number-of-people)
(seat-people-inner number-of-people (list 0)))
(define samples
(mh-query
500 1
(define final-arrangement (seat-people 50))
(length final-arrangement)
#t))
(hist samples "number of tables")
```
This program is asking the question, "How many tables are there when you seat 50 people?". It will then simulate it 500 times. Running that code produces something like this:
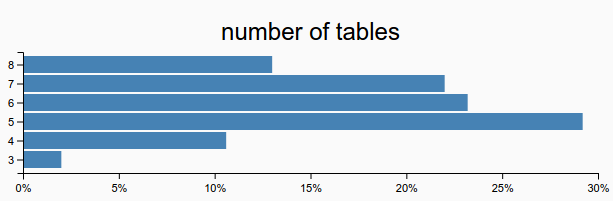
You could ask other questions like, "What is the chance that no one sits with the first person?"
```scheme
(define samples
(mh-query
500 1
(define final-arrangement (seat-people 50))
(eq? (last final-arrangement) 1)
#t))
(hist samples "no one sat with the first person")
```

"How many people are sitting alone, given that there is a table with 8 people on it?"
```scheme
(define (sample)
(rejection-query
(define final-arrangement (seat-people 50))
(length (filter (lambda (table-count) (eq? table-count 1)) final-arrangement))
(member 8 final-arrangement)))
(define samples (repeat 500 sample))
(hist samples "# sitting alone, >= one table with 8 people")
```
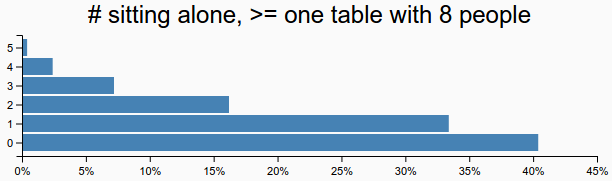
`rejection-query` will draw a sample and toss it if it doesn't fit the condition.